joi, 5 ianuarie 2017

Mathematical Tables and Formules

Comprehensive list of basic math formulas commonly used when doing basic math computation







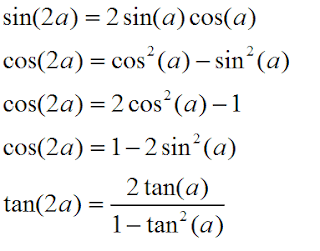
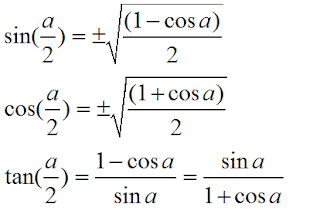
Average formula:
Let a1,a2,a3,......,an be a set of numbers, average = (a1 + a2 + a3,+......+ an)/n
Formula for a proportion:
In a proportion, the product of the extremes (ad) equal the product of the means(bc),
Thus, ad = bc
Percent:
Percent to fraction: x% = x/100
Percentage formula: Rate/100 = Percentage/base
Rate: The percent.
Base: The amount you are taking the percent of.
Percentage: The answer obtained by multiplying the base by the rate
Consumer math formulas:
Discount = list price × discount rate
Sale price = list price − discount
Discount rate = discount ÷ list price
Sales tax = price of item × tax rate
Interest = principal × rate of interest × time
Tips = cost of meals × tip rate
Commission = cost of service × commission rate
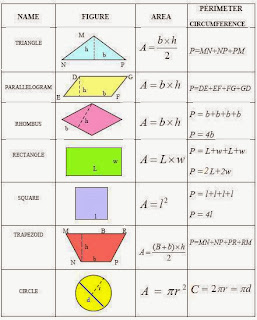
Geometry formulas:
Perimeter:
Perimeter of a square: s + s + s + s
s:length of one side
Perimeter of a rectangle: l + w + l + w
l: length
w: width
Perimeter of a triangle: a + b + c
a, b, and c: lengths of the 3 sides
Area:
Area of a square: s × s
s: length of one side
Area of a rectangle: l × w
l: length
w: width
Area of a triangle: (b × h)/2
b: length of base
h: length of height
Area of a trapezoid: (b1 + b2) × h/2
b1 and b2: parallel sides or the bases
h: length of height
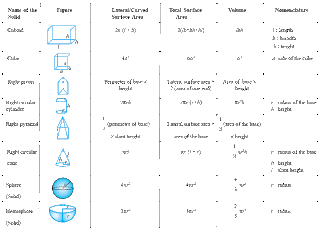
volume:
Volume of a cube: s × s × s
s: length of one side
Volume of a box: l × w × h
l: length
w: width
h: height
Volume of a sphere: (4/3) × pi × r3
pi: 3.14
r: radius of sphere
Volume of a triangular prism: area of triangle × Height = (1/2 base × height) ×
Height
base: length of the base of the triangle
height: height of the triangle
Height: height of the triangular prism
Volume of a cylinder:pi × r2 × Height
pi: 3.14
r: radius of the circle of the base
Height: height of the cylinder
Closure Property of Addition
Sum (or difference) of 2 real numbers equals a real number
Additive Identity
a + 0 = a
Additive Inverse
a + (-a) = 0
Associative of Addition
(a + b) + c = a + (b + c)
Commutative of Addition
a + b = b + a
Definition of Subtraction
a - b = a + (-b)
Closure Property of Multiplication
Product (or quotient if denominator (!=)0) of 2 reals equals a real number
Multiplicative Identity
a * 1 = a
Multiplicative Inverse
a * (1/a) = 1 (a (!=) 0)
(Multiplication times 0)
a * 0 = 0
Associative of Multiplication
(a * b) * c = a * (b * c) Commutative of Multiplication
a * b = b * a
Distributive Law
a(b + c) = ab + ac
Definition of Division
a / b = a(1/b)
Polynomial Identities
(a+b) 2 = a 2 + 2ab + b 2
(a+b)(c+d) = ac + ad + bc + bd
a 2 - b 2 = (a+b)(a-b) (Difference of squares)
a 3 (+-) b 3 = (a (+-) b)(a 2(-+) ab + b 2) (Sum and Difference of Cubes)
x 2 + (a+b)x + AB = (x + a)(x + b)
if ax 2 + bx + c = 0 then x = ( -b (+-)sqrt(b 2 - 4ac) ) / 2a (Quadratic Formula)
Exponential Identities
Powers
x a x b = x (a + b)
x a y a = (xy) a
(x a) b = x (ab)
x (a/b) = bth root of (x a) = ( bth (root)(x) ) a
x (-a) = 1 / x a
x (a - b) = x a / x b
Logarithms
y = logb(x) if and only if x=b y
logb(1) = 0
logb(b) = 1
logb(x*y) = logb(x) + logb(y)
logb(x/y) = logb(x) - logb(y)
logb(x n) = n logb(x)
logb(x) = logb(c) * logc(x) = logc(x) / logc(b)
Vector Notation: The lower case letters a-h, l-z denote scalars. Uppercase bold A-Z denote vectors. Lowercase bold i, j, k denote unit vectors.
 

denotes a vector with components a and b. denotes vector with n components of which are x1, x2, x3, ..,xn. |R| denotes the magnitude of the vector R.
b="" |a b="" | = magnitude of vector = sqrt(a 2+ b 2)

b="" || = sqrt(x12+ .. + xn2)


b="" + = a

b="" c="" d="" + = < x1+y1, .., xn+yn>


b="" c="" d="" k

b=""k =

. = ac + bd
p> . = x1 y1 + .. + xn yn>

R . S= |R| |S| cos theta(theta = angle between them)
R . S= S . R

(a R) . (bS) = (ab) R . S

R . (S + T)= R . S+ R . T

R . R = |R| 2

|R x S| = |R| |S| sin theta(theta = angle between both vectors). Direction of R x S is





perpendicular to A & B and according to the right hand rule.

| i j k |

R x S = | r1 r2 r3 | = / |r2 r3| |r3 r1| |r1 r2| \

| s1 s2 s3 | \ |s2 s3| , |s3 s1| , |s1 s2| /

S x R = - R x S

(a R) x S = R x (a S) = a (Rx S)

R x (S + T) = R x S + Rx T

R x R = 0 >

If a, b, c = angles between the unit vectors i, j,k and R Then the direction cosines are set by:

COs a = (R . i) / |R|; COs b = (R . j) / |R|; COs c = (R . k) / |R|

|R x S| = Area of parrallagram with sides Rand S.

Component of R in the direction of S = |R|COs theta = (R . S) / |S|(scalar result)

Projection of R in the direction of S = |R|COs theta = (R . S) S/ |S| 2 (vector result)

Complexity
Basic Operations

i = sqrt(-1)

i 2 = -1

1 / i = -i

i 4k = 1; i (4k+1) = i; i (4k+2) = -1; i (4k+3) = -i (k = integer)

sqrt( i ) = sqrt(1/2)+ sqrt(1/2) i

Complex Definitions of Functions and Operations

(a + bi) + (c + di) = (a+c) + (b + d) i

(a + BI) (c + DI) = ac + adi + bci + bdi 2 = (ac - bd) + (ad +bc) i

1/(a + BI) = a/(a 2 + b 2) - b/(a 2 + b 2) i

(a + BI) / (c + DI) = (ac + BD)/(c 2 + d 2) + (BC - ad)/(c 2 +d 2) i

a2 + b2 = (a + BI) (a - BI) (sum of squares)

e (i theta) = costheta + i sin theta

n (a + BI) = (COs(b ln n) + i sin(b ln n))n a

if z = r(COs theta+ i sin theta) then z n = r n ( COs ntheta+ i sin ntheta )(DeMoivre's Theorem)

if w = r(COs theta+ i sin theta);n=integer, then there are n complex nth roots (z) of w for k=0,1,..n-1:

z(k) = r (1/n) [ COs( (theta+ 2(PI)k)/n ) + i sin( (theta+ 2(PI)k)/n ) ]

if z = r (COs theta+ i sin theta) then ln(z) = ln r + i theta

sin(a + BI) = sin(a)cosh(b) + COs(a)sinh(b) i

COs(a + BI) = COs(a)cosh(b) - sin(a)sinh(b) i

tan(a + BI) = ( tan(a) + i tanh(b) ) / ( 1 - i tan(a) tanh(b)) = ( sech 2(b)tan(a) + sec 2(a)tanh(b) i ) / (1 + tan 2(a)tanh 2(b))

Table of Integrals

Power of x.

(integral)xn dx = x(n+1) / (n+1) + C

(n -1)

(integral)1/x dx = ln|x| + C

Exponential / Logarithmic

(integral)ex dx = ex + C

(integral)bx dx = bx / ln(b) + C

(integral)ln(x) dx = x ln(x) - x + C

Trigonometric

(integral)sin x dx = -cos x + C

(integral)csc x dx = - ln|CSC x + cot x| + C

(integral)COs x dx = sin x + C

(integral)sec x dx = ln|sec x + tan x| + C

(integral)tan x dx = -ln|COs x| + C

(integral)cot x dx = ln|sin x| + C

Trigonometric Result

(integral)COs x dx = sin x + C

(integral)CSC x cot x dx = - CSC x + C

(integral)sin x dx = COs x + C

(integral)sec x tan x dx = sec x + C

(integral)sec2 x dx = tan x + C

(integral)csc2 x dx = - cot x + C

Inverse Trigonometric

(integral)arcsin x dx = x arcsin x + sqrt(1-x2) + C

(integral)arccsc x dx = x arccos x - sqrt(1-x2) + C

(integral)arctan x dx = x arctan x - (1/2) ln(1+x2) + C

Inverse Trigonometric Result

(integral) dx

sqrt(1 - x2) = arcsin x + C

(integral) dx

x sqrt(x2 - 1) = arcsec|x| + C

(integral) dx

1 + x2 = arctan x + C

Useful Identities

arccos x = pi/2 - arcsin x (-1 <= x <= 1)

arccsc x = pi/2 - arcsec x (|x| >= 1)

arccot x = pi/2 - arctan x (for all x)

Hyperbolic

(integral)sinh x dx = cosh x + C

integral)csch x dx = ln |tanh(x/2)| + C

(integral)cosh x dx = sinh x + C

(integral)sech x dx = arctan (sinh x) + C

(integral)tanh x dx = ln (cosh x) + C

(integral)coth x dx = ln |sinh x| + C

Integral Identities

Formal Integral Definition:

(integral)(a to b) f(x) dx = lim (d -> 0) (sum) (k=1..n) f(X(k)) (x(k) - x(k-1)) when...

a = x0 < x1 < x2 < ... < xn = b

d = max (x1-x0, x2-x1, ... , xn - x(n-1))

x(k-1) <= X(k) <= x(k) k = 1, 2, ... , n

(integral)(a to b) F '(x) dx = F(b) - F(a) (Fundamental Theorem for integrals of derivatives)

(integral)a f(x) dx = a(integral) f(x) dx (if a is constant)

(integral)f(x) + g(x) dx = (integral)f(x) dx + (integral)g(x) dx

(integral)(a to b) f(x) dx = (integral)f(x) dx | (a b)

(integral)(a to b) f(x) dx + (integral)(b to c) f(x) dx = (integral)(a to c) f(x) dx

(integral)f(u) du/dx dx = (integral)f(u) du (integration by substitution)

Set Identities

Definitions:

Universal set : I

Empty set: ∅

Union of sets A∪B={x:x∈A or x∈B}

Intersection of sets

A∩B={x:x∈A and x∈B}

Complement

A′={x∈I:x/∈A}

Difference of sets A∖B={x:x∈A and x/∈B}

Cartesian product

A×B={(x,y):x∈A and y∈B}

Set identities involving union

Commutativity

A∪B=B∪A

Associativity

A∪(B∪C)=(A∪B)∪C

Idempotency

A∪A=A

Set identities involving intersection

Commutativity

A∩B=B∩A

Associativity

A∩(B∩C)=(A∩B)∩C

Idempotency

A∩A=A

Set identities involving union and intersection

Distributivity

A∪(B∩C)=(A∪B)∩(A∪C)

A∩(B∪C)=(A∩B)∪(A∩C)

Domination

A∩∅=∅

A∪I=I

Identity

A∪∅=∅

A∩I=A

Set identities involving union, intersection and complement

Complement of intersection and union

A∪A′=I

A∩A′=∅

De Morgan's laws

(A∪B)′=A′∩B ′

(A∩B)′=A′∪B ′

Set identities involving difference

B∖A=B∖(A∪B)

B∖A=B∩A′

A∖A=∅

(A∖B)∩C=(A∩C)∖(B∩C)

A′=I∖A

Sets of Numbers

Definitions:

N : Natural numbers

N0 : Whole numbers

Z : Integers

Z+ : Positive integers

Z− : Negative integers

Q : Rational numbers

C : Complex numbers

Formulas:

Natural numbers (counting numbers )

N={1,2,3,…}

Whole numbers ( counting numbers with zero )

N0={0,1,2,3,…}

Integers ( whole numbers and their opposites and zero )

Z={…,−2,−1,0,1,2,…}

Z+=N={1,2,…}

Z−={…,−3,−2,−1}

Z=Z−∪0∪Z

Irrational numbers: Non repeating and nonterminating integers

Real numbers: Union of rational and irrational numbers

Complex numbers:

C={x+iy | x∈R and y∈R}

N⊂N0⊂Z⊂Q⊂R⊂C

Complex numbers

Definitions:

A complex number is written as a+bi where a and b are real numbers an i, called the imaginary unit, has the property that i2=−1.

The complex numbers z=a+bi and z−=a−bi are called complex conjugate of each other.

Formulas:

Equality of complex numbers

a+bi=c+di⟺a=c and b=d

Addition of complex numbers

(a+bi)+(c+di)=(a+c)+(b+d)i

Subtraction of complex numbers

(a+bi)−(c+di)=(a−c)+(b−d)i

Multiplication of complex numbers

(a+bi)⋅(c+di)=(ac−bd)+(ad+bc)i

Division of complex numbers

a+bic+di=a+bic+di⋅c−dic−di=ac+bdc2+d2+bc−adc2+d2i

Polar form of complex numbers

a+bi=r⋅(cosθ+isinθ)

Multiplication and division of complex numbers in polar form

[r1(cosθ1+i⋅sinθ1)]⋅[r2(cosθ2+i⋅sinθ2)]=r1⋅r2[cos(θ1+θ2)+i⋅sin(θ1+θ2)]

r1(cosθ1+isinθ1)r2(cosθ2+isinθ2)=r1r2[cos(θ1−θ2)+i⋅sin(θ1−θ2)]

De Moivre's theorem

[r(cosθ+isinθ)]n=rn(cos(nθ)+isin(nθ))

Roots of complex numbers

[r(cosθ+isinθ)]1/n=r1/n(cosθ+2kπn+isinθ+2kπn) k=0,1,…,n−1

actoring and product formulas

Factoring Formulas

Factoring and product formulas

a2−b2=(a−b)(a+b)

a3−b3=(a−b)(a2+ab+b2)

a3+b3=(a+b)(a2−ab+b2)

a4−b4=(a−b)(a+b)(a2+b2)

a5−b5=(a−b)(a4+a3b+a2b2+ab3+b4)

Product Formulas

(a+b)2=a2+2ab+b2

(a−b)2=a2−2ab+b2

(a+b)3=a3+3a2b+3ab2+b3

(a−b)3=a3−3a2b+3ab2−b3

(a+b)4=a4+4a3b+6a2b2+4ab3+b4

(a−b)4=a4−4a3b+6a2b2−4ab3+b4

(a+b+c)2=a2+b2+c2+2ab+2ac+2bc

(a+b+c+...)2=a2+b2+c2+...+2(ab+ac+bc+...)

Solutions of algebraic equations

Quadric Equation: ax2+bx+c=0

Solutions (roots):

x1,2=−b±b2−4ac−−−−−−−√2a

If D=b2−4ac is the discriminant , then the roots are

1. real and unique if D>0

2. real and equal if D=0

3. complex conjugate if D<0 data-blogger-escaped-p=""> Cubic Equation: x3+a1x2+a2x+a3=0

Let

QRST=3a2−a219=9a1a2−27a3−2a3154=R+Q3+R2−−−−−−−√−−−−−−−−−−−−√3=R−Q3+R2−−−−−−−√−−−−−−−−−−−−√3

Then solutions (roots) of the cubic equation are:

x1x2x3=S+T−13a1=−12(S+T)−13a1+12i3√(S−T)=−12(S+T)−13a1−12i3√(S−T)

If D=Q3+R2 is the discriminant of the cubic equation, then:

1. one root is real and two complex conjugate if D>0

2. all roots are real and at last two are equal if D=0

3. all roots are real and unequal if D<0 data-blogger-escaped-p=""> Quartic Equation:x4+a1x3+a2x2+a3x+a4=0

Let y1 be a real root of the cubic equation

y3−a2y2+(a1a3−4a4)y+(4a2a4−a23−a21a4)=0

Then solutions of the quartic equation are the 4 roots of

z2+12(a1±a21−4a2+4y1−−−−−−−−−−−−√)z+12(y1±y21−4a4−−−−−−−√)=0

Exponents

Exponential Formulas

ap=a⋅a⋅…a}p (if p∈N)

a0=1 (if a≠0)

ar⋅as=ar+s

aras=ar−s

(ar)s=ar⋅s

(a⋅b)r=ar⋅br

(ab)r=arbr

a−r=1ar

ars=ar−−√s

Roots Formulas

Notation:

a,b : bases (a≥0,b≥0 if n=2k)

n,m: powers

Formulas (

a√n)n=a

(a√n)m=am−−−√n

a√n−−−√m=a√nm

(am−−−√n)p=anp−−−√n

am−−−√n=anp−−−√np

1a√n=an−1−−−−√na

ab−−√n=a√n⋅b√n

ab−−√n=a√nb√n


a√nb√m=ambn−−−√nm
p>a√n⋅b√m=ambn−−−−−√nm


a±b√−−−−−−√=a+a2−b−−−−−√2−−−−−−−−−−−√±a−a2−b−−−−−√2−−−−−−−−−−−√


1a√±b√=a√∓b√a−b


Logarithm formulas


y=logax⟺ay=x (a,x>0,a≠1)


loga1=0


logaa=1


loga(mn)=logam+logan


logamn=logam−logan


logamn=n⋅logam


logam=logbm⋅logab


logam=logbmlogba


logab=alogba


logax=lnalnx


Trigonometry Identities


Right-Triangle Definitions


Right-Triangle Definition


sinα=OppositeHypotenuse


cosα=AdjacentHypotenuse


tanα=OppositeAdjacent


cscα=1sinα=HypotenuseOpposite


secα=1cosα=HypotenuseAdjacent


cotα=1tanα=AdjacentOpposite


Reduction Formulas


sin(−x)=−sin(x)


cos(−x)=cos(x)


sin(π2−x)=cos(x)


cos(π2−x)=sin(x)

sin(π2+x)=cos(x)
cos(π2+x)=−sin(x)

sin(π−x)=sin(x)

cos(π−x)=−cos(x)

sin(π+x)=−sin(x)




cos(π+x)=−cos(x)

Basic Identities

sin2x+cos2x=1
p>tan2x+1=1cos2x

cot2x+1=1sin2x

Sum and Difference Formulas

sin(α+β)=sinα⋅cosβ+sinβ⋅cosα

sin(α−β)=sinα⋅cosβ−sinβ⋅cosα

cos(α+β)=cosα⋅cosβ−sinα⋅cosβ

cos(α−β)=cosα⋅cosβ+sinα⋅cosβ

tan(α+β)=tanα+tanβ1−tanα⋅tanβ

tan(α−β)=tanα−tanβ1+tanα⋅tanβ

Double Angle and Half Angle Formulas

sin(2α)=2⋅sinα⋅cosα

cos(2α)=cos2α−sin2α

tan(2α)=2tanα1−tan2α

sinα2=±1−cosα2−−−−−−−−√

cosα2=±1+cosα2−−−−−−−−√
tanα2=1−cosαsinα=sinα1−cosα

tanα2=±1+cosα1−cosα−−−−−−−−√

Other Useful Trig Formulas

Law of sines

sinαα=sinββ=sinγγ

Law of cosines

a2=b2+c2−2⋅b⋅c⋅cosαb2=a2+c2−2⋅a⋅c⋅cosβc2=a2+b2−2⋅a⋅b⋅cosγ

Area of triangle

A=12absinγ

Definitions of hyperbolic functions

sinhx=ex−e−x2

coshx=ex+e−x2

tanhx=ex−e−xex+e−x=sinhxcoshx
cschx=2ex−e−x=1sinhx


sechx=2ex+e−x=1coshx


cothx=ex+e−xex−e−x=coshxsinhx


Derivatives


ddxsinhx=coshx


ddxcoshx=sinhx


ddxtanhx=sech2x


ddxcschx=−cschx⋅cothx


ddxsechx=−sechx⋅tanhx


ddxcothx=−csch2x


Hyperbolic identities


cosh2x−sinh2x=1


tanh2x+sech2x=1


coth2x−csch2x=1


sinh(x±y)=sinhx⋅coshy±coshx⋅sinhy


cosh(x±y)=coshx⋅coshy±sinhx⋅sinhy


sinh(2⋅x)=2⋅sinhx⋅coshx


cosh(2⋅x)=cosh2x+sinh2x


sinh2x=−1+cosh2x2


cosh2x=1+cosh2x2


Inverse Hyperbolic functions


sinh−1x=ln(x+x2+1−−−−−√), x∈(−∞,∞)


cosh−1x=ln(x+x2−1−−−−−√), x∈[1,∞)


tanh−1x=12ln(1+x1−x), x∈(−1,1)


coth−1x=12ln(x+1x−1), x∈(−∞,−1)∪(1,∞)


sech−1x=ln(1+1−x2−−−−−√x), x∈(0,1]


csch−1x=ln(1x+1−x2−−−−−√|x|), x∈(−∞,0)∪(0,∞)


Derivatives of Inverse Hyperbolic functions


ddxsinh−1x=1x2+1−−−−−√


ddxcosh−1x=1x2−1−−−−−√


ddxtanh−1x=11−x2


ddxcsch−1x=−1|x|1+x2−−−−−√


ddxsech−1x=−1x1−x2−−−−−√


ddxcoth−1x=11−x2


Maths Formulas


(a + b)(a – b) = a2 – b2


(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)


(a ± b)2 = a2 + b2± 2ab


(a + b + c + d)2 = a2 + b2 + c2 + d2 + 2(ab + ac + ad + bc + bd + cd)


(a ± b)3 = a3 ± b3 ± 3ab(a ± b)


(a ± b)(a2 + b2 m ab) = a3 ± b3


(a + b + c)(a2 + b2 + c2 -ab – bc – ca) = a3 + b3 + c3 – 3abc =


1/2 (a + b + c)[(a - b)2 + (b - c)2 + (c - a)2]


when a + b + c = 0, a3 + b3 + c3 = 3abc


(x + a)(x + b) (x + c) = x3 + (a + b + c) x2 + (ab + bc + ac)x + abc


(x – a)(x – b) (x – c) = x3 – (a + b + c) x2 + (ab + bc + ac)x – abc


a4 + a2b2 + b4 = (a2 + ab + b2)( a2 – ab + b2)


a4 + b4 = (a2 – √2ab + b2)( a2 + √2ab + b2)


an + bn = (a + b) (a n-1 – a n-2 b + a n-3 b2 – a n-4 b3 +…….. + b n-1)


(valid only if n is odd)


an – bn = (a – b) (a n-1 + a n-2 b + a n-3 b2 + a n-4 b3 +……… + b n-1)

{where n ϵ N)

(a ± b)2n is always positive while -(a ± b)2n is always negative, for any real values of a and b

(a – b)2n = (b – a)2” and (a – b)2n+1 = – (b – a)2n+1

if α and β are the roots of equation ax2 + bx + c = 0, roots of cx” + bx + a = 0 are 1/α and 1/β.

if α and β are the roots of equation ax2 + bx + c = 0, roots of ax2 – bx + c = 0 are -α and -β.
< p>n(n + l)(2n + 1) is always divisible by 6.

32n leaves remainder = 1 when divided by 8

n3 + (n + 1 )3 + (n + 2 )3 is always divisible by 9

102n + 1 + 1 is always divisible by 11

n(n2- 1) is always divisible by 6

n2+ n is always even

23n-1 is always divisible by 7

152n-1 +l is always divisible by 16

n3 + 2n is always divisible by 3

34n – 4 3n is always divisible by 17

n! + 1 is not divisible by any number between 2 and n

(where n! = n (n – l)(n – 2)(n – 3)…….3.2.1)

for eg 5! = 5.4.3.2.1 = 120 and similarly 10! = 10.9.8…….2.1= 3628800

Product of n consecutive numbers is always divisible by n!.

If n is a positive integer and p is a prime, then np – n is divisible by p.

|x| = x if x ≥ 0 and |x| = – x if x ≤ 0.

Minimum value of a2.sec2Ɵ + b2.cosec2Ɵ is (a + b)2; (0° < Ɵ < 90°)

for eg. minimum value of 49 sec2Ɵ + 64.cosec2Ɵ is (7 + 8)2 = 225.

among all shapes with the same perimeter a circle has the largest area.

if one diagonal of a quadrilateral bisects the other, then it also bisects the quadrilateral.

sum of all the angles of a convex quadrilateral = (n – 2)180°

number of diagonals in a convex quadrilateral = 0.5n(n – 3)

let P, Q are the midpoints of the nonparallel sides BC and AD of a trapezium ABCD.Then,

ΔAPD = ΔCQB.









INDICES AND LOGARITHMS
am × a n = am + n (am ) n = a mn log( AB ) = log A + log B log( A/B ) = log A - log B log( A n ) = n log A a log b a = log c logc b 3
TRIGONOMETRIC IDENTITIES
tan A = sin A/ cos Asec A = 1 / cos Acosec A = 1 / sin Acot A = cos A/ sin A = 1 / tan Asin2 A + cos 2 A = 1sec2 A = 1 + tan 2 Acosec 2 A = 1 + cot 2 Asin( A ± B ) = sin A cos B ± cos A sin Bcos( A ± B ) = cos A cos B sin A sin Btan( A ± B ) = tan A± tan B 1 tan A tan Bsin 2A = 2 sin A cos Acos 2A = cos 2 A - sin 2 A = 2 cos 2 A - 1 = 1 - 2 sin2 Atan 2 A = 2tan A 1- tan 2 Asin 3A = 3 sin A - 4 sin3 Acos 3A = 4 cos 3 A - 3 cos Atan 3 A = 3 tan A- tan 3 A 1 - 3tan 2 Asin A + sin B = 2 sin A +B cos A-B 2 2
sin A - sin B = 2 cos A+ B sin A-B 2 2cos A + cos B = 2 cos A+ B cos A-B 2 2cos A - cos B = - 2 sin A + B sin A-B 2 22 sin A cos B = sin( A + B ) + sin( A - B )2 cos A sin B = sin( A + B ) - sin( A - B )2 cos A cos B = cos( A + B ) + cos( A - B )- 2 sin A sin B = cos( A + B ) - cos( A - B ) va sin x + b cos x = R sin( x + f ), where R = a 2 + b2 and cos f = a/R , sin f = b/R .If t = tan 1 x then sin x = 2t , cos x = 1 -t 2 . 2 1+ t2 1+ t2cos x = 1 ( eix + e-ix ) ; sin x = 1 (eix - -ix ) 2 2i eeix = cos x + i sin x ; e-ix = cos x - sin x i 5
COMPLEX NUMBERS v i= - 1 Note:- ‘ j ’ often used rather than ‘ i’.
Exponential Notation ei = cos + i sin
De Moivre’s theorem [r (cos + i sin )]n = rn (cos n + i sin n )nth roots of complex numbers If z = r i = r (cos + i sin ) then e vr z 1/n = ne i ( +2 kp ) /n , = 0 , ± 1, ± 2, ... k
HYPERBOLIC IDENTITIES cosh x = ( ex + e-x ) / 2 sinh x = ( ex - -x )/2 e tanh x = sinh x cosh x / sech x = 1 / cosh x cosech x = 1 / sinh x coth x = cosh x sinh x = 1 / tanh x / cosh i = cos x sinh i = i sin x x x cos i = cosh x sin i = i sinh x x x cosh 2 A - sinh 2 A = 1 sec 2 A = 1 - tanh 2 A h cosec 2 A = coth 2 A - 1 h 6
SERIESPowers of Natural Numbers
n n n k = 1 n ( n + 1) ; k = 1 n ( n + 1)(2 n + 1); 2 k3 = 1 n 2 (n + 1) 2 2 6 4k =1 k =1 k =1 n- 1 n
Arithmetic Sn = (a + k ) = { 2a + ( n - 1)d} d 2 k =0
Geometric (convergent for - 1 < r < 1) n- 1 a(1 - n ) a Sn = a k = = r 1rr,S - 8 1- k =0
rBinomial (convergent for |x| 1) < n! n! (1 + x )n = 1 + n + x 2 + ... + x r + ... x ( n - 2)!2! ( n - r )!r! n! n ( n - 1)( n - 2)... ( n - r + 1)where (n - r )!r ! = r!
Maclaurin series x2 xk f (x ) = f (0) + x (0) + f (0) + ... + f ( k ) (0) + R k +1 f 2! k! x k +1 where R k +1 = f ( k +1) ( x ) , 0 < < 1 ( k + 1)!
Taylor series h2 hk f ( a + h ) = f ( a) + hf ( a) + f ( a) + ... + f ( k ) (a ) + R k +1 2! k! h k +1 where R k +1 = f ( k +1) (a + h ) , 0 < < 1. (k + 1)!OR x - 0 )2 x - 0 )k ( k ) f (x ) = f ( x0 ) + ( x - 0 ) f (x 0 ) + ( x f (x 0 ) + ... + ( x f (x 0 ) + R k +1 x 2! k! x - 0 ) k +1 ( k +1) where R k +1 = ( x f (x 0 + ( x - 0 ) ), 0 < < 1 ( k + 1)! x 7
Special Power Series
\x2 x3 xr e =1+ x + x ... + ... (all x ) 2! + 3! + r! + 3 x5 7 - 1)r x2 r +1 sin x = x - - ... + ( ... (all x ) x 3! + 5! x 7! + (2 r + 1)! + x4 62 - 1) r x 2r cos x = 1 - - ... + ( ... (all x ) x 2! + 4! x 6! + (2r )! + x3 x5 x7 tan x = x + ... ( |x| p ) 3 + 2 15 + 17315 + < 2 x3 .3 x5 .3.5 x7 sin - 1 x = x +1 2 3 + 1 2. 4 5 + 1 2.4.6 7 + .3.5.... (2 n - 1) x 2n +1 ... + 1 ... ( |x| 1) 2.4. 6.... (2 n ) 2n + 1 + < x5 3 7 x2 n +1 tan - 1 x = x - - ... + ( - 1) n ... ( |x| 1) x 3+ 5 x 7+ 2n + 1 + < x3 2 4 xn n (1 + x ) = x - - ... + ( - 1) n +1 + ... ( - 1 < x = 1) x 2+ 3 x 4+ n x3 x5 x7 x 2 n +1 sinh x = x + ... + ... (all x ) 3! + 5! + 7! + (2n + 1)! + x2 x4 x6 x 2n cosh x = 1 + ... + ... (all x ) 2! + 4! + 6! + (2n )! + x5 17x 7 3 tanh x = x - - ... ( |x| p ) x 3 + 2 15 315 + < 2 1 x3 .3 x5 1.3.5 x 7 sinh - 1 x = x - - 2 3 + 1 2.4 5 2.4.6 7 + 1.3.5... (2n - 1) x2n +1 ... + ( - 1) n ... ( |x| 1) 2.4.6... 2n 2n + 1 + < x3 x5 x7 2 n +1 tanh - 1 x = x+ ... x ... ( |x| 1) 3+ 5+ 7+ 2n + 1 + < 8
DERIVATIVES
function derivativexn n n- 1 xxex eax ( a > 0) ax na n 1 x xloga x 1 x nasin x cos xcos x - sin xtan x sec2 xcosec x - cosec x cot xsec x sec x tan xcot x - cosec 2 x 1sin- 1 x v 1- 2 x 1cos- 1 x - v 1- 2 x 1tan - 1 x 1 + x2sinh x cosh xcosh x sinh xtanh x sech 2 xcosech x - cosech x coth xsech x - sech x tanh xcoth x - cosech 2 x 1sinh - 1 x v 1 + x2cosh - 1 x (x > 1) 1 v x 2 - 1tanh - 1 x ( |x| 1) 1 < 1- 2 x 1coth - 1 x (|x| 1) - > x2 - 1 9
Laws of Exponents
(am)(an) = am+n
(ab)m = ambm
(am)n = amn
Fractional Exponents
a0 = 1
(am)/(an) = am-n
a-m= 1/(am)
Quadratic Formula
In an equation like ax2 + bx + c = 0
You can solve for x using the Quadratic Formula: Quadratic Formulas
Binomial Theorem
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 ...and so on...
Difference of Squares
a2 - b2 = (a - b)(a + b)
Rules of Zero
0/x = 0 where x is not equal to 0.
a0 = 1
0a = 0
a*0 = 0
a/0 is undefined (you can't do it)
The Greek alphabet
Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω
α β γ δ ε ζ η ϑ θ ι κ λ μ ν ξ ο π ρ σ τ υ φ ϕ χ ψ ω
Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω
α β γ δ ε ζ η ϑ θ ι κ λ μ ν ξ ο π ρ σ τ υ φ ϕ χ ψ ω
Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω
α β γ δ ε ζ η ϑ θ ι κ λ μ ν ξ ο π ρ σ τ υ φ ϕ χ ψ ω
Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω
α β γ δ ε ζ η ϑ θ ι κ λ μ ν ξ ο π ρ σ τ υ φ ϕ χ ψ ω
|r| = √(x2 + y2 + z2) |r| = √(x2 + y2 + z2)
|r| = sqrt(x^2 + y^2 + z^2)
lim
n→∞ an
lim
n→∞ an
{ limit n -> infinity } a_n
∞
∏
n = 0 an
∞
∏
n = 0 an
{ product from n=0 to infinity } a_n
∞
∑
n = 0 an
∞
∑
n = 0 an
{ sum from n=0 to infinity } a_n
∆u = n
∑
i = 1 ∂2u/∂xi2
∆u = n
∑
i = 1 ∂2u/∂xi2
Laplacian of u = { sum from i=1 to n } d^2u / dx_i^2
b
∫
a f(x) dx
b
∫
a f(x) dx
b
⌠
⌡
a f(x) dx
b
⌠
⌡
a f(x) dx
{ integral from a to b } f(x) dx
+∞
∫
−∞ exp(−x²) dx = √π
+∞
∫
−∞ exp(−x²) dx = √π
{ integral from -infinity to +infinity } exp(-x^2) dx = sqrt pi
√5 − 1 = 2
2 √5 + 1
( sqrt 5 - 1) / 2 = 2 / (sqrt 5 + 1)
Factorial (n!)
The factorial of n is denoted by n! and calculated by the product of integer numbers
from 1 to n.
For n>0,
n! = 1×2×3×4×...×n
For n=0,
0! = 1
Factorial definition formula
n!=\begin{Bmatrix}1 & ,n=0 \\ \prod_{k=1}^{n}k & ,n>0\end{matrix}
Examples:
1! = 1
2! = 1×2 = 2
3! = 1×2×3 = 6
4! = 1×2×3×4 = 24
5! = 1×2×3×4×5 = 120
Recursive factorial formula
n! = n×(n-1)!
Example:
5! = 5×(5-1)! = 5×4! = 5×24 = 120
Striling's approximation
n!\approx \sqrt{2\pi n}\cdot n^n\cdot e^{-n}
Example:
5! ≈ √2π5·55·e-5 = 118.019
Factorial table
Number
n
Factorial
n!
0 1
1 1
2 2
3 6
4 24
5 120
6 720
7 5040
8 40320
9 362880
10 3628800
11 3.991680x107
12 4.790016x108
13 6.227021x109
14 8.717829x1010
15 1.307674x1012
16 2.092279x1013
17 3.556874x1014
18 6.402374x1015
19 1.216451x1017
20 2.432902x1018
C program for factorial calculation
double factorial(unsigned int n)
{
double fact=1.0;
if( n > 1 )
for(unsigned int k=2; k<=n; k++)
fact = fact*k;
return f;
}
Logarithm definition
When b is raised to the power of y is equal x:
b y = x
Then the base b logarithm of x is equal to y:
logb(x) = y
For example when:
24 = 16
Then
log2(16) = 4
Logarithm as inverse function of exponential function
The logarithmic function,
y = logb(x)
is the inverse function of the exponential function,
x = by
So if we calculate the exponential function of the logarithm of x (x>0),
f (f -1(x)) = blogb(x) = x
Or if we calculate the logarithm of the exponential function of x,
f -1(f (x)) = logb(bx) = x
Natural logarithm (ln)
Natural logarithm is a logarithm to the base e:
ln(x) = loge(x)
When e constant is the number:
e=\lim_{x\to \infty }(1+\frac{1}{n})^{n}=\lim_{x\to 0 }(1+n)^\frac{1}{n}=2.71828183...
See: Natural logarithm
Inverse logarithm calculation
The inverse logarithm (or anti logarithm) is calculated by raising the base b to the
logarithm y:
x = log-1(y) = b y
Logarithmic function
The logarithmic function has the basic form of:
f (x) = logb(x)
Logarithm rules
Rule name Rule
Logarithm product rule
logb(x ∙ y) = logb(x) + logb(y)
Logarithm quotient rule
logb(x / y) = logb(x) - logb(y)
Logarithm power rule
logb(x y) = y ∙ logb(x)
Logarithm base switch rule
logb(c) = 1 / logc(b)
Logarithm base change rule
logb(x) = logc(x) / logc(b)
Derivative of logarithm
f (x) = logb(x) ⇒ f ' (x) = 1 / ( x ln(b) )
Integral of logarithm
∫ logb(x) dx = x ∙ ( logb(x) - 1 / ln(b) ) + C
Logarithm of negative number
logb(x)is undefined when x≤ 0
Logarithm of 0
logb(0) is undefined
\lim_{x\to 0^+}\textup{log}_b(x)=-\infty
Logarithm of 1
logb(1) = 0
Logarithm of the base
logb(b) = 1
Logarithm of infinity
lim logb(∞) = ∞,when x→∞
See: Logarithm rules
Logarithm product rule
The logarithm of the multiplication of x and y is the sum of logarithm of x and logarithm of y.
logb(x ∙ y) = logb(x) + logb(y)
For example:
log10(3 ∙ 7) = log10(3) + log10(7)
Logarithm quotient rule
The logarithm of the division of x and y is the difference of logarithm of x and logarithm of y.
logb(x / y) = logb(x) - logb(y)
For example:
log10(3 / 7) = log10(3) - log10(7)
Logarithm power rule
The logarithm of x raised to the power of y is y times the logarithm of x.
logb(x y) = y ∙ logb(x)
For example:
log10(28) = 8∙ log10(2)
Logarithm base switch rule
The base b logarithm of c is 1 divided by the base c logarithm of b.
logb(c) = 1 / logc(b)
For example:
log2(8) = 1 / log8(2)
Logarithm base change rule
The base b logarithm of x is base c logarithm of x divided by the base c logarithm of b.
logb(x) = logc(x) / logc(b)
For example, in order to calculate log2(8) in calculator, we need to change the base to 10:
log2(8) = log10(8) / log10(2)
See: log base change rule
Logarithm of negative number
The base b real logarithm of x when x<=0 is undefined when x is negative or equal to zero:
logb(x) is undefined when x ≤ 0
See: log of negative number
Logarithm of 0
The base b logarithm of zero is undefined:
logb(0) is undefined
The limit of the base b logarithm of x, when x approaches zero, is minus infinity: \lim_{x\to 0^+}\textup{log}_b(x)=-\infty
See: log of zero
Logarithm of 1
The base b logarithm of one is zero:
logb(1) = 0
For example, teh base two logarithm of one is zero:
log2(1) = 0
See: log of one
Logarithm of infinity
The limit of the base b logarithm of x, when x approaches infinity, is equal to infinity:
lim logb(x) = ∞, when x→∞
See: log of infinity
Logarithm of the base
The base b logarithm of b is one:
logb(b) = 1
For example, the base two logarithm of two is one:
log2(2) = 1
Logarithm derivative
When
f (x) = logb(x)
Then the derivative of f(x):
f ' (x) = 1 / ( x ln(b) )
See: log derivative
Logarithm integral
The integral of logarithm of x:
∫ logb(x) dx = x ∙ ( logb(x) - 1 / ln(b) ) + C
For example:
∫ log2(x) dx = x ∙ ( log2(x) - 1 / ln(2) ) + C
Logarithm approximation
log2(x) ≈ n + (x/2n - 1) ,
Logarithm problems and answers
Problem #1
Find x for
log2(x) + log2(x-3) = 2
Solution:
Using the product rule:
log2(x∙(x-3)) = 2
Changing the logarithm form according to the logarithm definition:
x∙(x-3) = 22
Or
x2-3x-4 = 0
Solving the quadratic equation:
x1,2 = [3±√(9+16) ] / 2 = [3±5] / 2 = 4,-1
Since the logarithm is not defined for negative numbers, the answer is:
x = 4
Problem #2
Find x for
log3(x+2) - log3(x) = 2
Solution:
Using the quotient rule:
log3((x+2) / x) = 2
Changing the logarithm form according to the logarithm definition:
(x+2)/x = 32
Or
x+2 = 9x
Or
8x = 2
Or
x = 0.25
Graph of log(x)
log(x) is not defined for real non positive values of x:
Logarithms table
x log10x log2x logex
0 undefined undefined undefined
0+ - ∞ - ∞ - ∞
0.0001 -4.000000 -13.287712 -9.210340
0.001 -3.000000 -9.965784 -6.907755
0.01 -2.000000 -6.643856 -4.605170
0.1 -1.000000 -3.321928 -2.302585
1 0.000000 0.000000 0.000000
2 0.301030 1.000000 0.693147
3 0.477121 1.584963 1.098612
4 0.602060 2.000000 1.386294
5 0.698970 2.321928 1.609438
6 0.778151 2.584963 1.791759
7 0.845098 2.807355 1.945910
8 0.903090 3.000000 2.079442
9 0.954243 3.169925 2.197225
10 1.000000 3.321928 2.302585
20 1.301030 4.321928 2.995732
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 3.688879
50 1.698970 5.643856 3.912023
60 1.778151 5.906991 4.094345
70 1.845098 6.129283 4.248495
80 1.903090 6.321928 4.382027
90 1.954243 6.491853 4.499810
100 2.000000 6.643856 4.605170
200 2.301030 7.643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5.991465
500 2.698970 8.965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9.643856 6.684612
900 2.954243 9.813781 6.802395
1000 3.000000 9.965784 6.907755
10000 4.000000 13.287712 9.210340




A Table of the Common Logarithm

The table below lists the common logarithms (with base 10) for numbers between 1 and 10.
The logarithm is denoted in bold face. For instance, the first entry in the third column means that the common log of 2.00 is 0.3010300.


1.0000.000000002.000.30103003.000.47712134.000.60206005.000.69897006.000.77815137.000.84509808.000.90309009.000.9542425
1.0010.000434082.010.30319613.010.47856654.010.60314445.010.69983776.010.77887457.010.84571808.010.90363259.010.9547248
1.0020.000867722.020.30535143.020.48000694.020.60422615.020.70070376.020.77959657.020.84633718.020.90417449.020.9552065
1.0030.001300932.030.30749603.030.48144264.030.60530505.030.70156806.030.78031737.030.84695538.030.90471559.030.9556878
1.0040.001733712.040.30963023.040.48287364.040.60638145.040.70243056.040.78103697.040.84757278.040.90525609.040.9561684
1.0050.002166062.050.31175393.050.48429984.050.60745505.050.70329146.050.78175547.050.84818918.050.90579599.050.9566486
1.0060.002597982.060.31386723.060.48572144.060.60852605.060.70415056.060.78247267.060.84880478.060.90633509.060.9571282
1.0070.003029472.070.31597033.070.48713844.070.60959445.070.70500806.070.78318877.070.84941948.070.90687359.070.9576073
1.0080.003460532.080.31806333.080.48855074.080.61066025.080.70586376.080.78390367.080.85003338.080.90741149.080.9580858
1.0090.003891172.090.32014633.090.48995854.090.61172335.090.70671786.090.78461737.090.85064628.090.90794859.090.9585639
1.0100.004321371.100.04139272.100.32221933.100.49136174.100.61278395.100.70757026.100.78532987.100.85125838.100.90848509.100.9590414
1.0110.004751161.110.04532302.110.32428253.110.49276044.110.61384185.110.70842096.110.78604127.110.85186968.110.90902099.110.9595184
1.0120.005180511.120.04921802.120.32633593.120.49415464.120.61489725.120.70927006.120.78675147.120.85248008.120.90955609.120.9599948
1.0130.005609451.130.05307842.130.32837963.130.49554434.130.61595015.130.71011746.130.78746057.130.85308958.130.91009059.130.9604708
1.0140.006037951.140.05690492.140.33041383.140.49692964.140.61700035.140.71096316.140.78816847.140.85369828.140.91062449.140.9609462
1.0150.006466041.150.06069782.150.33243853.150.49831064.150.61804815.150.71180726.150.78887517.150.85430608.150.91115769.150.9614211
1.0160.006893711.160.06445802.160.33445383.160.49968714.160.61909335.160.71264976.160.78958077.160.85491308.160.91169029.160.9618955
1.0170.007320951.170.06818592.170.33645973.170.50105934.170.62013615.170.71349056.170.79028527.170.85551928.170.91222219.170.9623693
1.0180.007747781.180.07188202.180.33845653.180.50242714.180.62117635.180.71432986.180.79098857.180.85612448.180.91275339.180.9628427
1.0190.008174181.190.07554702.190.34044413.190.50379074.190.62221405.190.71516746.190.79169067.190.85672898.190.91328399.190.9633155
1.0200.008600171.200.07918122.200.34242273.200.50515004.200.62324935.200.71600336.200.79239177.200.85733258.200.91381399.200.9637878
1.0210.009025741.210.08278542.210.34439233.210.50650504.210.62428215.210.71683776.210.79309167.210.85793538.210.91434329.210.9642596
1.0220.009450901.220.08635982.220.34635303.220.50785594.220.62531255.220.71767056.220.79379047.220.85853728.220.91487189.220.9647309
1.0230.009875631.230.08990512.230.34830493.230.50920254.230.62634045.230.71850176.230.79448807.230.85913838.230.91539989.230.9652017
1.0240.010299961.240.09342172.240.35024803.240.51054504.240.62736595.240.71933136.240.79518467.240.85973868.240.91592729.240.9656720
1.0250.010723871.250.09691002.250.35218253.250.51188344.250.62838895.250.72015936.250.79588007.250.86033808.250.91645399.250.9661417
1.0260.011147361.260.10037052.260.35410843.260.51321764.260.62940965.260.72098576.260.79657437.260.86093668.260.91698009.260.9666110
1.0270.011570441.270.10380372.270.35602593.270.51454784.270.63042795.270.72181066.270.79726757.270.86153448.270.91750559.270.9670797
1.0280.011993111.280.10721002.280.35793483.280.51587384.280.63144385.280.72263396.280.79795967.280.86213148.280.91803039.280.9675480
1.0290.012415371.290.11058972.290.35983553.290.51719594.290.63245735.290.72345576.290.79865067.290.86272758.290.91855459.290.9680157
1.0300.012837221.300.11394342.300.36172783.300.51851394.300.63346855.300.72427596.300.79934057.300.86332298.300.91907819.300.9684829
1.0310.013258671.310.11727132.310.36361203.310.51982804.310.63447735.310.72509456.310.80002947.310.86391748.310.91960109.310.9689497
1.0320.013679701.320.12057392.320.36548803.320.52113814.320.63548375.320.72591166.320.80071717.320.86451118.320.92012339.320.9694159
1.0330.014100321.330.12385162.330.36735593.330.52244424.330.63648795.330.72672726.330.80140377.330.86510408.330.92064509.330.9698816
1.0340.014520541.340.12710482.340.36921593.340.52374654.340.63748975.340.72754136.340.80208937.340.86569618.340.92116619.340.9703469
1.0350.014940351.350.13033382.350.37106793.350.52504484.350.63848935.350.72835386.350.80277377.350.86628738.350.92168659.350.9708116
1.0360.015359761.360.13353892.360.37291203.360.52633934.360.63948655.360.72916486.360.80345717.360.86687788.360.92220639.360.9712758
1.0370.015778761.370.13672062.370.37474833.370.52762994.370.64048145.370.72997436.370.80413947.370.86746758.370.92272559.370.9717396
1.0380.016197351.380.13987912.380.37657703.380.52891674.380.64147415.380.73078236.380.80482077.380.86805648.380.92324409.380.9722028
1.0390.016615551.390.14301482.390.37839793.390.53019974.390.64246455.390.73158886.390.80550097.390.86864448.390.92376209.390.9726656
1.0400.017033341.400.14612802.400.38021123.400.53147894.400.64345275.400.73239386.400.80618007.400.86923178.400.92427939.400.9731279
1.0410.017450731.410.14921912.410.38201703.410.53275444.410.64443865.410.73319736.410.80685807.410.86981828.410.92479609.410.9735896
1.0420.017867721.420.15228832.420.38381543.420.53402614.420.64542235.420.73399936.420.80753507.420.87040398.420.92531219.420.9740509
1.0430.018284311.430.15533602.430.38560633.430.53529414.430.64640375.430.73479986.430.80821107.430.87098888.430.92582769.430.9745117
1.0440.018700501.440.15836252.440.38738983.440.53655844.440.64738305.440.73559896.440.80888597.440.87157298.440.92634249.440.9749720
1.0450.019116291.450.16136802.450.38916613.450.53781914.450.64836005.450.73639656.450.80955977.450.87215638.450.92685679.450.9754318
1.0460.019531681.460.16435292.460.39093513.460.53907614.460.64933495.460.73719266.460.81023257.460.87273888.460.92737049.460.9758911
1.0470.019946681.470.16731732.470.39269703.470.54032954.470.65030755.470.73798736.470.81090437.470.87332068.470.92788349.470.9763500
1.0480.020361281.480.17026172.480.39445173.480.54157924.480.65127805.480.73878066.480.81157507.480.87390168.480.92839599.480.9768083
1.0490.020775491.490.17318632.490.39619933.490.54282544.490.65224635.490.73957236.490.81224477.490.87448188.490.92890779.490.9772662
1.0500.021189301.500.17609132.500.39794003.500.54406804.500.65321255.500.74036276.500.81291347.500.87506138.500.92941899.500.9777236
1.0510.021602721.510.17897692.510.39967373.510.54530714.510.65417655.510.74115166.510.81358107.510.87563998.510.92992969.510.9781805
1.0520.022015741.520.18184362.520.40140053.520.54654274.520.65513845.520.74193916.520.81424767.520.87621788.520.93043969.520.9786369
1.0530.022428371.530.18469142.530.40312053.530.54777474.530.65609825.530.74272516.530.81491327.530.87679508.530.93094909.530.9790929
1.0540.022840611.540.18752072.540.40483373.540.54900334.540.65705595.540.74350986.540.81557777.540.87737138.540.93145799.540.9795484
1.0550.023252461.550.19033172.550.40654023.550.55022844.550.65801145.550.74429306.550.81624137.550.87794708.550.93196619.550.9800034
1.0560.023663921.560.19312462.560.40824003.560.55145004.560.65896485.560.74507486.560.81690387.560.87852188.560.93247389.560.9804579
1.0570.024074991.570.19589972.570.40993313.570.55266824.570.65991625.570.74585526.570.81756547.570.87909598.570.93298089.570.9809119
1.0580.024485671.580.19865712.580.41161973.580.55388304.580.66086555.580.74663426.580.81822597.580.87966928.580.93348739.580.9813655
1.0590.024895961.590.20139712.590.41329983.590.55509444.590.66181275.590.74741186.590.81888547.590.88024188.590.93399329.590.9818186
1.0600.025305871.600.20412002.600.41497333.600.55630254.600.66275785.600.74818806.600.81954397.600.88081368.600.93449859.600.9822712
1.0610.025715381.610.20682592.610.41664053.610.55750724.610.66370095.610.74896296.610.82020157.610.88138478.610.93500329.610.9827234
1.0620.026124521.620.20951502.620.41830133.620.55870864.620.66464205.620.74973636.620.82085807.620.88195508.620.93550739.620.9831751
1.0630.026533261.630.21218762.630.41995573.630.55990664.630.66558105.630.75050846.630.82151357.630.88252458.630.93601089.630.9836263
1.0640.026941631.640.21484382.640.42160393.640.56110144.640.66651805.640.75127916.640.82216817.640.88309348.640.93651379.640.9840770
1.0650.027349611.650.21748392.650.42324593.650.56229294.650.66745305.650.75204846.650.82282167.650.88366148.650.93701619.650.9845273
1.0660.027757201.660.22010812.660.42488163.660.56348114.660.66838595.660.75281646.660.82347427.660.88422888.660.93751799.660.9849771
1.0670.028164421.670.22271652.670.42651133.670.56466614.670.66931695.670.75358316.670.82412587.670.88479548.670.93801919.670.9854265
1.0680.028571251.680.22530932.680.42813483.680.56584784.680.67024595.680.75434836.680.82477657.680.88536128.680.93851979.680.9858754
1.0690.028977711.690.22788672.690.42975233.690.56702644.690.67117285.690.75511236.690.82542617.690.88592638.690.93901989.690.9863238
1.0700.029383781.700.23044892.700.43136383.700.56820174.700.67209795.700.75587496.700.82607487.700.88649078.700.93951939.700.9867717
1.0710.029789471.710.23299612.710.43296933.710.56937394.710.67302095.710.75663616.710.82672257.710.88705448.710.94001829.710.9872192
1.0720.030194791.720.23552842.720.43456893.720.57054294.720.67394205.720.75739606.720.82736937.720.88761738.720.94051659.720.9876663
1.0730.030599721.730.23804612.730.43616263.730.57170884.730.67486115.730.75815466.730.82801517.730.88817958.730.94101429.730.9881128
1.0740.031004281.740.24054922.740.43775063.740.57287164.740.67577835.740.75891196.740.82865997.740.88874108.740.94151149.740.9885590
1.0750.031408461.750.24303802.750.43933273.750.57403134.750.67669365.750.75966786.750.82930387.750.88930178.750.94200819.750.9890046
1.0760.031812271.760.24551272.760.44090913.760.57518784.760.67760705.760.76042256.760.82994677.760.88986178.760.94250419.760.9894498
1.0770.032215701.770.24797332.770.44247983.770.57634144.770.67851845.770.76117586.770.83058877.770.89042108.770.94299969.770.9898946
1.0780.032618761.780.25042002.780.44404483.780.57749184.780.67942795.780.76192786.780.83122977.780.89097968.780.94349459.780.9903389
1.0790.033021441.790.25285302.790.44560423.790.57863924.790.68033555.790.76267866.790.83186987.790.89153758.790.94398899.790.9907827
1.0800.033423761.800.25527252.800.44715803.800.57978364.800.68124125.800.76342806.800.83250897.800.89209468.800.94448279.800.9912261
1.0810.033825691.810.25767862.810.44870633.810.58092504.810.68214515.810.76417616.810.83314717.810.89265108.810.94497599.810.9916690
1.0820.034227261.820.26007142.820.45024913.820.58206344.820.68304705.820.76492306.820.83378447.820.89320688.820.94546869.820.9921115
1.0830.034628461.830.26245112.830.45178643.830.58319884.830.68394715.830.76566866.830.83442077.830.89376188.830.94596079.830.9925535
1.0840.035029281.840.26481782.840.45331833.840.58433124.840.68484545.840.76641286.840.83505617.840.89431618.840.94645239.840.9929951
1.0850.035429741.850.26717172.850.45484493.850.58546074.850.68574175.850.76715596.850.83569067.850.89486978.850.94694339.850.9934362
1.0860.035829831.860.26951292.860.45636603.860.58658734.860.68663635.860.76789766.860.83632417.860.89542258.860.94743379.860.9938769
1.0870.036229541.870.27184162.870.45788193.870.58771104.870.68752905.870.76863816.870.83695677.870.89597478.870.94792369.870.9943172
1.0880.036628901.880.27415782.880.45939253.880.58883174.880.68841985.880.76937736.880.83758847.880.89652628.880.94841309.880.9947569
1.0890.037027881.890.27646182.890.46089783.890.58994964.890.68930895.890.77011536.890.83821927.890.89707708.890.94890189.890.9951963
1.0900.037426501.900.27875362.900.46239803.900.59106464.900.69019615.900.77085206.900.83884917.900.89762718.900.94939009.900.9956352
1.0910.037824751.910.28103342.910.46389303.910.59217684.910.69108155.910.77158756.910.83947807.910.89817658.910.94987779.910.9960737
1.0920.038222641.920.28330122.920.46538293.920.59328614.920.69196515.920.77232176.920.84010617.920.89872528.920.95036499.920.9965117
1.0930.038620161.930.28555732.930.46686763.930.59439264.930.69284695.930.77305476.930.84073327.930.89927328.930.95085159.930.9969492
1.0940.039017321.940.28780172.940.46834733.940.59549624.940.69372695.940.77378646.940.84135957.940.89982058.940.95133759.940.9973864
1.0950.039414121.950.29003462.950.46982203.950.59659714.950.69460525.950.77451706.950.84198487.950.90036718.950.95182309.950.9978231
1.0960.039810551.960.29225612.960.47129173.960.59769524.960.69548175.960.77524636.960.84260927.960.90091318.960.95230809.960.9982593
1.0970.040206631.970.29446622.970.47275643.970.59879054.970.69635645.970.77597436.970.84323287.970.90145838.970.95279249.970.9986952
1.0980.040602341.980.29666522.980.47421633.980.59988314.980.69722935.980.77670126.980.84385547.980.90200298.980.95327639.980.9991305
1.099 0.040997691.990.29885312.990.47567123.990.60097294.990.69810055.990.77742686.990.84447727.990.90254688.990.95375979.990.9995655



Geometry formulas:

Perimeter:

Perimeter of a square: s + s + s + s
s:length of one side

Perimeter of a rectangle: l + w + l + w
l: length
w: width

Perimeter of a triangle: a + b + c
a, b, and c: lengths of the 3 sides

Area:

Area of a square: s × s
s: length of one side

Area of a rectangle: l × w
l: length
w: width

Area of a triangle: (b × h)/2
b: length of base
h: length of height

Area of a trapezoid: (b1 + b2) × h/2
b1 and b2: parallel sides or the bases
h: length of height

volume:

Volume of a cube: s × s × s
s: length of one side

Volume of a box: l × w × h
l: length
w: width
h: height

Volume of a sphere: (4/3) × pi × r3
pi: 3.14
r: radius of sphere

Volume of a triangular prism: area of triangle × Height = (1/2 base × height) × Height
base: length of the base of the triangle
height: height of the triangle
Height: height of the triangular prism

Volume of a cylinder:pi × r2 × Height
pi: 3.14
r: radius of the circle of the base
Height: height of the cylinder


1. Decimal Multipliers

10 1deka (da)10 -1deci (d)
10 2hecto (h)10 -2centi (c)
10 3kilo (k)10 -3milli (m)
10 6mega (M)10 -6micro (u)
10 9giga (G)10 -9nano (n)
10 12tera (T)10 -12pico (p)
10 15peta (P)10 -15femto (f)
10 18exa (E)10 -18atto (a)


2. Series.

Maclaurin Series.

1.      e x = 1 + x + x 2 / 2! + ... + x n / n! + ...
for all x
2.       sin x = x - x 3 / 3! + x 5 / 5! - x 7 / 7! + ...
for all x
3.       cos x = 1 - x 2 / 2! + x 4 / 4! - x 6 / 6! + ...
for all x
4.       ln(1 + x) = x - x 2 / 2 + x 3 / 3 -... + (-1) n+1 x n / n + ...
for (-1 < x <= 1)
5.       tan x = x + (1/3) x 3 + (2/15) x 5 + (17/315) x 7 + ...
for (-Pi/2 < x < Pi/2)
6.       arcsin x = x + (1/2) x 3 / 3 + (1.3/2.4) x 5 / 5 + (1.3.5/2.4.6) x 7 / 7 + ...
for (-1 < x < 1)
7.       arctan x = x - x 3 / 3 + x 5 / 5 - ...
for (-1 < x < 1)
8.       sinh x = x + x 3 / 3! + x 5 / 5! + x 7 / 7! + ...
for all x
9.       cosh x = x + x 2 / 2! + x 4 / 4! + x 6 / 6! + ...
for all x
10.       arcsinh x = x - (1/2) x 3 / 3 + (1.3/2.4) x 5 / 5 - (1.3.5/2.4.6) x 7 / 7 + ...
for (-1 < x < 1)
11.       1 / (1 - x) = 1 + x + x 2 + x 3 + ...
for (-1 < x < 1)


Arithmetic Series.

12.       Sn = a + (a + d) + (a + 2d)+...+(a + [n-1]d)

= (n/2)[first term + last term]

= (n/2)[a + (a+[n - 1]d)

= n(a + [n - 1]d)

Geometric Series.

13.       Sn = a + a r + a r 2 + a r 3 +...+ a r n-1 = a (1 - r n)/(1 - r)

Integer Series.

14.       1 + 2 + 3 + ... + n = (1 / 2) n (n + 1)

15.       1 2 + 2 2 + 3 2 + ... + n 2 = (1 / 6) n (n + 1)(2n + 1)

15.       1 3 + 2 3 + 3 3 + ... + n 3 = [ (1 / 2) n (n + 1) ] 2

3. Factorial, Permutations and Combinations.

1.       n factorial = n ! = n.(n-1).(n-2)...2.1

2.      Permuatations of n objects taken r at the time:

n P r = n ! / [ (n - r) ! ]


3.      Combinations of n objects taken r at the time:

n C r = n ! / [ r ! (n - r) ! ]


4. Binomial Expansion (Formula).

1. If n is a positive integer, we can expand (x + y) n as follows

(x + y) n = n C 0 x n + n C 1 x n - 1 y + n C 2 x n - 2 y 2 + ... + n C n y n

The general term n C r is given by

n C r = n ! / [ r ! (n - r) ! ]


5. Trigonometric Formulas.

Sum / Difference of Angles Formulas.

1.       cos(A + B) = cos A cos B - sin A sin B

2.       cos(A - B) = cos A cos B + sin A sin B

3.       sin(A + B) = sin A cos B + cos A sin B

4.       sin(A - B) = sin A cos B - cos A sin B

5.       tan(A + B) = [ tan A + tan B ] / [ 1 - tan A tan B]

6.       tan(A - B) = [ tan A - tan B ] / [ 1 + tan A tan B]

Sum / Difference of Trigonometric Functions Formulas.

7.       sin A + sin B = 2 sin [ (A + B) / 2 ] cos [ (A - B) / 2 ]

8.       sin A - sin B = 2 cos [ (A + B) / 2 ] sin [ (A - B) / 2 ]

9.       cos A + cos B = 2 cos [ (A + B) / 2 ] cos [ (A - B) / 2 ]

10.       cos A - cos B = - 2 sin [ (A + B) / 2 ] sin [ (A - B) / 2 ]

Product of Trigonometric Functions Formulas.

11.       2 sin A cos B = sin (A + B) + sin (A - B)

12.       2 cos A sin B = sin (A + B) - sin (A - B)

13.       2 cos A cos B = cos (A + B) + cos (A - B)

14.       2 sin A sin B = - cos (A + B) + cos (A - B)

Multiple Angles Formulas.

15.       sin 2A = 2 sin A cos A

16.       cos 2A = cos 2 A - sin 2 A = 2 cos 2 A - 1 = 1 - 2 sin 2 A

17.       sin 3A = 3 sin A - 4 sin 3 A

18.       cos 3A = 4 cos 3 A - 3 cos A

Power Reducing Formulas.

19.       sin 2 A = (1/2) [ 1 - cos 2A ]

19.       cos 2 A = (1/2) [ 1 + cos 2A ]
A table of the first derivates of common functions and used in calculus is presented.
f(x)d [f(x)] / dx
x nn x n - 1
e xe x
ln (x)1 / x
sin xcos x
cos x- sin x
tan xsec 2x
cot x- csc 2x
sec xsec x tan x
csc x- csc x cot x
arcsin x1 / sqrt (1 - x 2)
arccos x- 1 / sqrt (1 - x 2)
arctan x1 / (1 + x 2)
sinh xcosh x
cosh xsinh x
tanh xsech 2 x
coth x- csch 2 x
sech x- sech x tanh x
csch x- csch x coth x
arcsinh x1 / sqrt [x 2 + 1 ]
arccosh x1 / sqrt [x 2 - 1 ]
arctanh x1 / [ 1 - x 2 ]


Table of Laplace Transforms.


f(t) F(s)
1 1 / s
t 1 / s 2
t n n! / s n+1 , (n = 1,2,3...)
t 1/2 Pi 1/2 / 2s 3/2
t -1/2 (Pi / s) 1/2
e -a t 1 / (s + a)
t e -a t 1 / (s + a) 2
sin a t a / (s 2 + a 2)
t sin a t 2 a s / (s 2 + a 2) 2
e -at sin b t b / (s + a) 2 + b 2
cos a t s / (s 2 + a 2)
t cos a t (s 2 - a 2) / (s 2 + a 2) 2
e -at cos b t (s + a) / (s + a) 2 + b 2
sinh a t a / (s 2 - a 2)
cosh a t s / (s 2 - a 2)
1 - cos a t a 2 / s (s 2 + a 2)
(2 / t)( t - cos a t) ln [ (s 2 + a 2) / s 2 ]
(2 / t)( t - cosh a t) ln [ (s 2 - a 2) / s 2 ]
(1 / t)( sin a t) arctan(a / s)

Table of Fourier Transforms.


Publicat de la Niciun comentariu:
Abonați-vă la: Postări (Atom)
f(t)F(w)
u(t) e -a t , a > 01 / (a + i w)
1 for - a <= t <= a
and 0 otherwise		2 sin (w a) / w
A (constant)2 p A d (w)
d (t)1
d (t - a)e -i w a
cos (a t)p [ d (w + a) + d (w - a) ]
sin (a t)(p / i) [ d (w - a) - d (w + a) ]
e i a t2 p [ d (w - a) ]
f'(t)i w f(w)
f"(t)(i w) 2 f(w)
t f(t)i d [f(w)] / dw
t 2 f(t)i 2 d 2[f(w)] / dw 2